need in 10 hours

IT 236 

MELISSA SIMPSOM

1:Since the website is suppose to attract the audience I think the best practice is the description. In other words, make sure that the information the user is looking for is there without confusing them. When I go to a website to look for information I am not looking for contacts or about us at the time. I want to find the information that I need to search out. I believe that web designers should put the most important pages first in their description. When all of the important pages are together an in order the user can find the information easily.

2:Since the website is suppose to attract the audience I think the best practice is the description. In other words, make sure that the information the user is looking for is there without confusing them. When I go to a website to look for information I am not looking for contacts or about us at the time. I want to find the information that I need to search out. I believe that web designers should put the most important pages first in their description. When all of the important pages are together an in order the user can find the information easily.

3:In my opinion I think the best practice is to keep it simple, do not over complicate getting from page to page. This will make it easy for the visitor to find what they want and may lead them to look at more that is on your site. A good example is the Missouri Department of Conservation’s website, it is packed with information but can be very hard to find one item or subject you are looking for, because you have to go though some many pages, tabs and links to get there. Simple, easy to read tabs that will take the visitor where they want to go and find the information they are looking for, will help them want to come back to the site. I think to many designers want to make a site look and feel more sophisticated then they need too.

IT 240

4:   I pretty much went through all the parts of a TCP/IP plan that I thought were important. I am therefore going to talk about why you should register your network in this post. For people who are newer at this like me, I was wondering why it is necessary to register your network. I found out that one reason is so that you can get a network number because you cannot arbitrarily make one up for yourself and you need one so that other people and networks like the Internet can recognize you. You also do it in order to register your domain, but I have not found out why you need to do that yet?

5:You bring up a good point about the MAC address on the device being referenced.  I am used to hearing about MAC reservations.  From what I am understanding about it is that the server will recognize the MAC address rather than the IP address and it will keep reassigning the same IP address based on the MAC address.  I see this as a form of using a static IP address.  What are your thoughts on this??

6: Hi Again Phillip,

For IP addresses if you want to use what is referred to as “Internet Addressable” space, you register or reserve your IP network really so that no one else will use them and create potential conflicts.  And the same is true of a domain name.  There is a registry so that only one entity can use any particular domain name.

 There are two types of ciphers – Block and Stream. Block is used to encrypt a block of bits at one time. Stream cipher is used to encrypt one bit at a time. 

• Modes of CiphersUnderstanding Modes
  
  Electronic Code Book (ECB) Mode

  This mode is a most straightforward way of processing a series of sequentially listed message blocks.
  Operation
  The user takes the first block of plaintext and encrypts it with the key to produce the first block of ciphertext.
  He then takes the second block of plaintext and follows the same process with same key and so on so forth.
  The ECB mode is deterministic, that is, if plaintext block P1, P2,…, Pm are encrypted twice under the same key, the output ciphertext blocks will be the same

  Cipher Block Chaining (CBC) Mode
  CBC mode of operation provides message dependence for generating ciphertext and makes the system non-deterministic.
  Operation
  The operation of CBC mode is depicted in the following illustration. The steps are as follows −
  Load the n-bit Initialization Vector (IV) in the top register.
  XOR the n-bit plaintext block with data value in top register.
  Encrypt the result of XOR operation with underlying block cipher with key K.
  Feed ciphertext block into top register and continue the operation till all plaintext blocks are processed.
  For decryption, IV data is XORed with first ciphertext block decrypted. The first ciphertext block is also fed into to register replacing IV for decrypting next ciphertext block.

  Output Feedback (OFB) Mode
  It involves feeding the successive output blocks from the underlying block cipher back to it. These feedback blocks provide string of bits to feed the encryption algorithm which act as the key-stream generator as in case of CFB mode.
  The key stream generated is XOR-ed with the plaintext blocks. The OFB mode requires an IV as the initial random n-bit input block. The IV need not be secret.

  Counter (CTR) Mode
  It can be considered as a counter-based version of CFB mode without the feedback. In this mode, both the sender and receiver need to access to a reliable counter, which computes a new shared value each time a ciphertext block is exchanged. This shared counter is not necessarily a secret value, but challenge is that both sides must keep the counter synchronized.
  Operation
  Both encryption and decryption in CTR mode are depicted in the following illustration. Steps in operation are −
  Load the initial counter value in the top register is the same for both the sender and the receiver. It plays the same role as the IV in CFB (and CBC) mode.
  Encrypt the contents of the counter with the key and place the result in the bottom register.
  Take the first plaintext block P1 and XOR this to the contents of the bottom register. The result of this is C1. Send C1 to the receiver and update the counter. The counter update replaces the ciphertext feedback in CFB mode.
  Continue in this manner until the last plaintext block has been encrypted.
  The decryption is the reverse process. The ciphertext block is XORed with the output of encrypted contents of counter value. After decryption of each ciphertext block counter is updated as in case of encryption.

  (Tutorial.com)

• Weakness of DES cipherThe launch a brute force on DES, the attacker would need to search 2^56 keys. That is a search for a needle in a haystack of 72 quadrillion straws. In 1977 that was considered an impossible computational task. In 1999 a special-purpose DES search engine combined with 100,000 personal computers on the Internet to find a DES challenge key in 22 hours.  

  FIPS 46-3, Data Encryption Standard (DES), was withdrawn on May 19, 2005 because the cryptographic algorithm no longer provided the security that is needed to protect Federal government information. DES is no longer an Approved algorithm. It was replaces temporarily by 3DES and later by AES

• Applying CBC ModeCBC-Mode

  CBC mode for DES –>

  1. Generation of an Initial Vector (Called an IV).

  (there is a few steps here that I am skipping for simplicity)

  2. This IV is XOR with the Clear Text

  3. The resulting ciphered text is used as the seed to generate the next encryption key for the next block.

  

• Course ProjectFor this project, you will need to pick a CURRENT topic in Cryptography and proposed a 5-page research paper. You paper will consist of an introduction, a literature review, a methodology and a result. Submit your proposal in the drop box.

• Galois Finite FieldGalois Fields or Finite FIelds

  Galois Fields

  Supposed we look at three numbers like 6 3 9 (IN THE DECIMAL BASE)

  If we look at these types of numbers  as a  decimal value, it is six hundred and thirty nine…right?

  SO, it is 6 X 10^2 + 3 X 10^1   + 9 X 10^0 = 600 + 30 + 9 = 639

  IN BINARY BASE

  10101011

  1X2^7 + 0X2^6 + 1X2^5 + 0X2^4 1X2^3 + 0X2^2 + 1X2^1 + 1X2^0

  Remember X^0 = 1

  128 + 0 + 32 + 0 + 8 + 0 + 2 + 1 = 171

  SO FAR…SO GOOD

  Let’s expand this concept more

  Let’s consider the number 5 7 2 (Still decimal)

  Based on what we learned above 572–> 5X^2 + 7X^1 + 2X^0

  BUT HERE IS THE WRENCH IN GALOIS FIELD

  Suppose we are adding 5 7 2 + 6 7 3

  We are looking at this in the DECIMAL SPACE

  5 7 2

  6 7 3

  You start with 2 + 3 = 5 (right!)

  Now let focus on the 7 + 7 = 14 –>you must now drop the 1 and keep the 4. We do not carry over the 1

  Same thing with the 5 + 6 = 11 –>you must now drop the 1 and keep the 1. We do not carry over the 1

  The answer is

  5 7 2

  6 7 3

  1 4 5 –>HA! (This is the trick)

  Well, we would never use BASE 10 in Galois field, we would use a Prime numbers

  Suppose we take the binary number  

  1 0 1 1 0 1 0 1 –>State of your clear text (One byte)

  1 0 0 1 1 0 1 1 –>KEY

  Remember here 1 + 1 = 2 but in base 2 and Galois field, this is equal to 0   (suppose you were looking at 5 + 5 = 10 à You would drop the 1 and keep the 0.

  1 0 1 1 0 1 0 1

  1 0 0 1 1 0 1 1

  0 0 1 0 1 1 1 0

  THINK OF THIS AS AN XOR <–

  0 0 –> 0

  0 1 –> 1

  1 0 –> 1

  1 1 –> 0

  I THINK WE HAVE THE ADDITION UNDER CONTROL — Right?

• DOT MATRIXWe know what PRODUCTS are. Now I am adding something new called DOT PRODUCTS. Well, a dot product applies to VECTORS. Well, what are Vectors?

  Think of a vectors as  a set of numbers ( 6    7   2)  – > this is a vector with 3 elements. Remember, MATRIX from college algebra and your high school teacher told you to remember MATRIX and you will see it again, well, today is the day. A VECTOR can be a ROW or a COLUMN of a MATRIX.

  If this make sense, I am ready to define DOT PRODUCT 

• ProductPRODUCT (not DOT Product)

  MULTIPLICATION IN GALOIS FIELD

  Suppose we need to multiply two POLYNOMIALS

  (x^5 + X^3 + X^2 + X^1) times (X^4 + X^3 + X^2)

  What do you usually do in Algebra?

  X^5(X^4 + X^3 + X^2) + X^3(X^4 + X^3 + X^2) + X^2(X^4 + X^3 + X^2) + X^1(X^4 + X^3 + X^2)

  THIS IS A LOT OF WORK

  Let’s try again

  (x^5 + X^3 + X^2 + X^1) times (X^4 + X^3 + X^2)

  

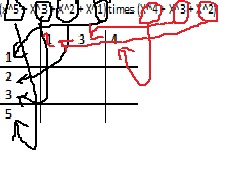
  23411 + 2 = 31 + 3 = 41 + 4 = 522 + 2 = 42 + 3 = 52 + 4 = 633 + 2 = 53 + 3 = 63 + 4 = 755 + 2 = 75 + 3 = 85 + 4 = 9

  Now it gets tricky

  We need to count the numbers (SUM)

  How many 9s? -> 1 (do not touch)

  How many 8s? -> 1 (do not touch)

  How many 7s? -> 2 -> NOW MODULUS 2 (binary) -> 0

  (Think of it this way -> if your count is EVEN, it becomes Zero and if it is ODD, the count is 1)

  How many 6s? -> 2 (even) -> 0

  How many 5s? -> 3 (odd) -> 1

  How many 4s? -> 2 (even) -> 0

  How many 3s? -> 1 (odd) -> 1

  How many 2s? -> 0 (even) -> 0

  REMEMBER WHERE WE STARTED:

  (x^5 + X^3 + X^2 + X^1) times (X^4 + X^3 + X^2)

  I am going to REWRITE

  (1X^5 + 0X^4 + 1X^3 + 1X^2 + 1X^1 + 0X^0) times (0X^5 + 1X^4 + 1X^3 + 1X^2 + 0X^1 + 0X^0)

  REMEMBER the underlined portions are ZEROs

  NOW, WE ARE GOING TO READ THE COEEFICIENTS

  (1 0 1 1 1 0) times ( 0 1 1 1 0 0 ) = 0 1 0 1 0 0 0 (THIS IS WHAT YOU HAVE ABOVE)

  I USED THIS EXAMPLE RANDOMLY BUT WE WANT TO LIMIT EVERYTHING TO ONE BYTE. IN OUR EXAMPLE, WE ARE GOOD SINCE WE HAVE LESS THAN 8 BITS  BUT WHAT IF THE RESULT WAS BIGGER THAN 8 BITS.

  What if our product was – 10101010100? This is bigger than one byte and it would not fit. FOR AES WE WANT EVERYTHING TO FIT IN ONE BYTE (One character).

  NOW we have to perform a Polynomial Reduction in Galois FIELD.

  THE MAGIC AND THE FACINATING PART OF THE ALGORITHM IS TO DIVIDE BY

  X^8 + X^4 + X^3 + X^1 + X^0 ( I am not sure how they came up with this polynomial – they are genius)

  REWRITING -> 1X^8 + 0X^7 + 0X^6 +0X^5 + 1X^4 + 1X^3 +0X^2 + 1X^1 + 1X^0

  Remember LONG DIVISION – We are going to use it in the next section.

• THE AMAZING REDUCTIONTHE AMAZING REDUCTION

  Let me see how to do the reduction.

  Let start with
  1010101010100 <- Clear text

  we have a total of eleven bits here.

  We are going to divide by X^8 + X^4 + X^3 + X^1 + X^0 (THE MAGIC POLYNOMIAL)

  Now let’s add the missing terms

  1X^8 +0X^7 + 0X^6 + 0X^5 + 1X^4 + 1X^3 + 0X^2 + 1X^1 + 1X^0

  So pulling the coefficient

  1 0 0 0 1 1 0 1 1

  REMEMBER WHAT WE ARE TRYING TO DO – TAKE

  1010101010100
  REDUCE to an 8-bit string

  According to AES, there is a magic formula – DIVIDE BY 1 0 0 0 1 1 0 1 1 (In GALOIS FILED)

  LIKE I SAID YESTERDAY – WE ARE going to do LONG DIVISION LIKE YOU DID IN HIGH SCHOOL OR JUNIOR HIGH SCHOOL. LET’s DO it. DIVIDING IS ALSO XOR in Galois Field

  1 0 1 0 1 0 1 0 1 0 1 0 0 <- ORIGINAL STRING
  1 0 0 0 1 1 0 1 1 <- REDUCER
  0 0 1 0 0 1 1 1 0 ( DO YOU REMEMBER HOW WE GET THIS STRING?)
  Now, notice the 0 1 0 0 was not used

  Now take the BOLD part (resulting from the XOR) and concatenate 0 1 0 0
  0 0 1 0 0 1 1 1 0 0 1 0 0
  Just in plain Black and White ->
  0 0 1 0 0 1 1 1 0 0 1 0 0 (THE BOLD + THE UNDERLINED)

  IS THIS A REDUCTION? <- YES, YES – YOU CAN DROP THE LEADING ZEROs, you will get

  1 0 0 1 1 1 0 0 1 0 0

  LET DO IT AGAIN and the rest is yours
  1 0 0 1 1 1 0 0 1 0 0 (the underlined  is unused)
  1 0 0 0 1 1 0 1 1 <- REDUCER
  0 0 0 1 0 0 0 1 0 0 0 <- Bring the unused 0 0 down
  0 0 0 1 0 0 0 1 0 0 0  Drop leading zeros
  You have 1 0 0 0 1 0 0 0
  WE DID IT!!!!!!
  COUNT IT  — 8-bit string

  AMAZING 

• THE ENCRYPTIONTHE ENCRYPTION

  The final stages of EAS Encryption

  When encrypting with AES, we only need to multiply by the Galois fields for 1, 2 and 3. The interesting part about this multiplication, it is already done for us. It is everywhere on the internet. I will show you the tables in a few minutes.

  A few things to remember –

  1. Multiply a Galois field by a Galois field for 1 – you get the same thing. It is like multiplying a number by 1. You get the same number back.
  2. Multiply by two or three are different. The original values des change. We can multiply or we can use the look up tables.
  3. There are two tables that are available MUL2 and MUL3.
  4. Remember the resulting values have to be MOD 100011011  Do you remember why? This is the reducer to make the result fit in a byte

  Let’s look at the word ‘what’ and apply AES to it

  W is a 57 in HEX – represented by 0x57
  h is a 68 in HEX – represented by 0x68
  a is a 61 in HEX – represented by 0x61
  t is a 74 in HEX – – represented by 0x74

  Now we have to take the DOT PRODUCT and it is complex.
  0x57
  0x68 [ 0x02 0x03 0x01 0x01 ]
  0x61
  0x74

  5 = 0101 (in bits)
  7 = 0111 (in bits)
  57 = 01010111 (Or use your scientific calculator)

  NOW
  How about the 02? -> (10)

  Now multiple the 01010111 by 10 (0x57 times 0x02 – HEX) (remember you did this before)

  X^6 + x^4 + x^2 + x^1 + x^0 multiply by X^1

  0 1
  1 2
  2 3
  4 5
  6 7

  Now we count
  How many

  7 – 1

  6 — 0
  5 — 1
  4 — 0
  3 — 1
  2 — 1
  1 – 0

  So 0x57 DOT 0x02 = 1 0 1 0 1 1 0

  Now do you need to reduce 

  THE ANSWER IS NO.

  Why  because the bits fit in a BYTE

  NO REDUCER NEEDED.

  I have one more post to finish with AES

 Submit a 5 page paper (APA style) detailing the how Blockchain technology can be implemented to reduce ad fraud and cost while meeting consumers’ increasing expectation for excellent customer service? 

Sources :

• PDF attached 
• “What Blockchain Could Mean for Marketing” https://hbr.org/2018/05/what-blockchain-could-mean-for-marketing 
• A Clearer Picture http://c2claritymedia.com/wp-content/uploads/accountability-transparency-in-media-today.pdf
• Competitive Info: Digital Ad Fraud To Hit $22B By 2020 http://www.insideradio.com/free/competitive-info-digital-ad-fraud-to-hit-b-by/article_6d3c6608-a815-11e7-9e40-bbd2e6133207.html
• Are You Ready to Meet Customer Expectations in 2018? http://fieldservicenews.com/ready-meet-customer-expectations-2018/

hi want a voting feature for answers to add in faq project that i have done using php storm,laravel and sqlite.  require adding a field(s) to a model(s), a updated query to use the new field such as to sort by votes, and an updated UI, so the feature can be used by an application user and tests should also be done and then deploy it heroku